Master Ratio & Proportion: Smart Tricks for CA Foundation Success!

MATHEMATICS: RATIO AND PROPORTION: EASY TRICKS TO SOLVE MATH PROBLEMS IN CA FOUNDATION

Introduction
Ratio and proportion are fundamental concepts in mathematics, forming a crucial part of the CA Foundation syllabus. Mastering this topic helps students solve problems quickly and accurately, not only in exams but also in real-life applications like finance, accounting, and business calculations. With the right strategies and shortcuts, ratio and proportion problems can become one of the easiest sections in the quantitative part of CA Foundation. This blog explains key concepts, common problem types, and effective tricks to solve them efficiently.

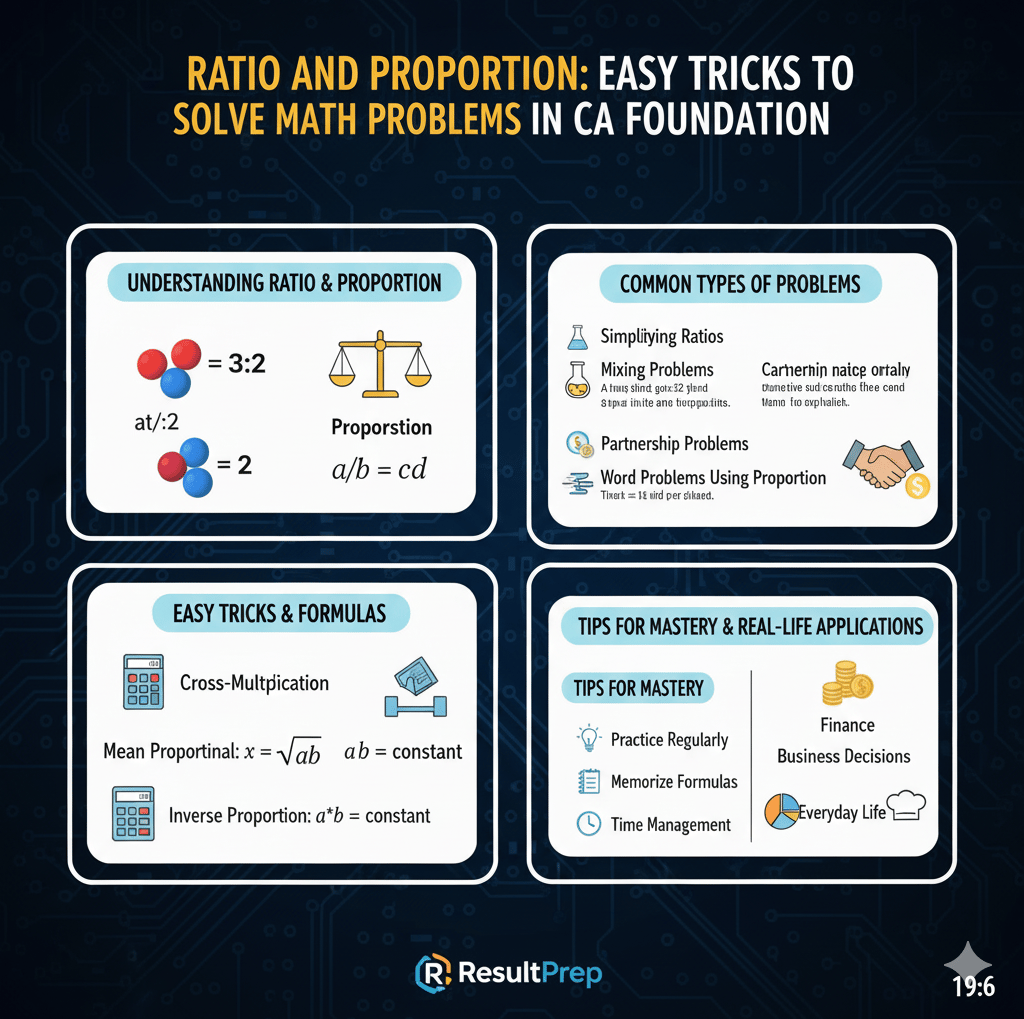
Understanding Ratio and Proportion
Ratio is a relationship between two or more quantities, showing how many times, one value contains or is contained within another.

Example: The ratio of boys to girls in a class is 3:2. This means for every 3 boys, there are 2 girls.

Proportion is an equation stating that two ratios are equal.
Example: If a:b = c:d, then a/b = c/d. This relationship is the foundation for solving many CA Foundation problems.

Basic Formulas and Concepts

1. Mean Proportional: If a:x = x:b, then x² = ab, so x = √(ab)

2. Inverse Proportion: If one quantity increases, the other decreases so that their product remains constant: a*b = constant

3. Direct Proportion: If two quantities increase or decrease together, a:b = c:d

Common Types of Problems in CA Foundation

1. Simplifying Ratios:
Example: Find the simplified ratio of 24:36.
Solution: Divide both terms by their GCD (12), so 24:36 = 2:3

2. Mixing Problems:
These involve combining two or more quantities in a given ratio.
Example: Mix two types of sugar in the ratio 3:5. How much of each type is needed to get 32 kg?
Solution: Total parts = 3 + 5 = 8
Sugar1 = 32 3/8 = 12 kg, Sugar2 = 32 5/8 = 20 kg

3. Partnership Problems:
Problems where capital, time, or profit sharing is involved in a ratio.
Example: A and B invest in a business in the ratio 2:3. Total profit is 50,000. Share of A = 50,000 * 2/5 = 20,000

4. Word Problems Using Proportion:
These often involve speed, distance, time, or population ratios.
Example: If 5 workers can complete a task in 12 days, how many days will 8 workers take?
Solution: Inverse proportion: 512 = 8x → x = 7.5 days

Easy Tricks to Solve Ratio and Proportion

1. Cross-Multiplication: Always check proportion problems using cross-multiplication for quick solutions.

2. Convert Ratios to Fractions: Working with fractions simplifies calculations.

3. Use Total Parts Method: For mixture and partnership problems, divide the total into parts according to the ratio.

4. Shortcut for Inverse Proportion: Multiply the first quantity by the second and equate it to the product of the other pair.

5. Check Sum of Parts: For profit-sharing, mixing, and population problems, always ensure the total matches the sum of individual parts.

Tips to Master Ratio and Proportion for CA Foundation

• Practice regularly: Solve multiple examples of each type to gain speed.

• Memorize key formulas: Ensure formulas like mean proportional, direct, and inverse proportion are remembered.

• Use Diagrams: Visual representation helps in understanding mixing and sharing problems.

• Time Management: Learn to solve problems quickly using shortcuts to save time during exams.

• Revise Frequently: Keep a formula sheet for quick revision before exams.

Real-Life Applications
Understanding ratio and proportion is not just academic; it has practical relevance:

• Finance and Accounting: Profit-sharing, investment analysis, and cost allocation often use ratios.

• Business Decisions: Mixing raw materials, workforce distribution, and production planning involve proportion calculations.

• Everyday Life: Cooking recipes, budgeting, and comparing quantities rely on ratio concepts.

Conclusion
Mastering ratio and proportion is essential for scoring well in CA Foundation mathematics. By understanding basic concepts, practicing different types of problems, and using smart shortcuts, students can increase speed, accuracy, and confidence.

At ResultPrep Coaching, we provide step-by-step guidance, practice exercises, and exam-focused strategies to help students master ratio and proportion efficiently. With the right practice and techniques, aspirants can solve complex problems effortlessly and achieve top marks in the CA Foundation exam.

📞 Call: 8970007497
🌐 Visit: www.resultprep.com